第10回 - ソート(3)
第10回では,以下の項目に関して学ぶ.
- 完全2分木
- ヒープソート
課題1: 木
木(tree)とは,それに格納されている各要素(節と呼ぶ)が階層関係(親子関係)を持つデータ構造である.階層関係における上位(親:parent)の節と下位(子:child)の節が枝で結合されている.
最も上位にある(親を持たない)節を根(root)と呼ぶ.木には根が1つだけ存在する.最も下位にある(子を持たない)節を葉(leaf)と呼ぶ.木の例を図10.1に示す.
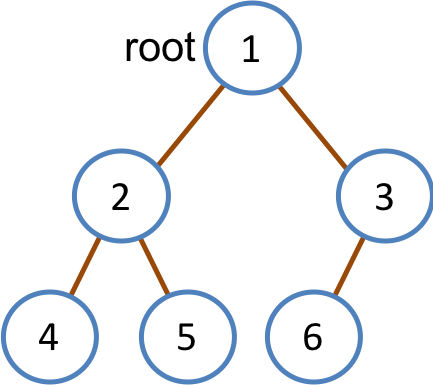
図10.1:木の例
節1は根,節4,節5,節6は葉である.また,節2と節3の親は節1である.反対に,節2と節3は節1の子である.
ここでは,各節が最大2つの子を持つ2分木(bainary tree)を考える.図10.1は2分木を表している.2分木の節は,以下に示す構造体で表現できる.
struct node {
int value;
struct node *left;
struct node *right;
};
left は左側の子,right は右側の子,value は格納する整数値を指す.子が存在しない場合は,left や right を NULL とする.
木において,すべての節は根からたどることができるので,根 root を持つ木を以下の構造体で表現する.
struct tree {
struct node *root;
};
いま,木を実現するために,heap-check.c に,以下に示す3つの関数を用意した.
(1) 空の木(根を持たない)を生成する.
struct tree *create_tree();
(2) 整数の値 value を格納した節を生成する.
struct node *create_node(int value);
(3) tree の節に格納されている整数の値を画面に表示する.
void print_tree(struct tree *tree);
これらの関数を利用するためには,heaptree-common.h をインクルードし,heap-check.o と queue.o をリンクすること.
上記の3つの関数を用いて,図10.1の木を構築するテスト関数test1()をprog10-1.cに記述せよ.さらに,図10.1以外の木を構築するテスト関数を追加せよ.
課題2: 完全2分木とヒープ
木において,根から節に到達する際に通る枝の数を,その節の深さという.根から葉に至るすべての節が2つの子を持ち,さらに,すべての葉が根から等しい深さを持つ2分木を完全2分木(complete binary tree)という.完全2分木は、左右の節の数が等しく,木の深さをnとすれば節の数は2nとなる.
厳密には,完全2分木において,すべての葉は等しい深さを持つ.ただし,例外的に,他の葉に比べて深さが1だけ大きい葉が存在する場合,それらの葉をできるだけ左に寄せた木も完全2分木とみなされる.図10.2の木は,完全2分木である.
木の節をたどる方法には,図10.2に示す横型(幅優先: bread-first)探索と縦型(深さ優先: depth-first)探索がある.
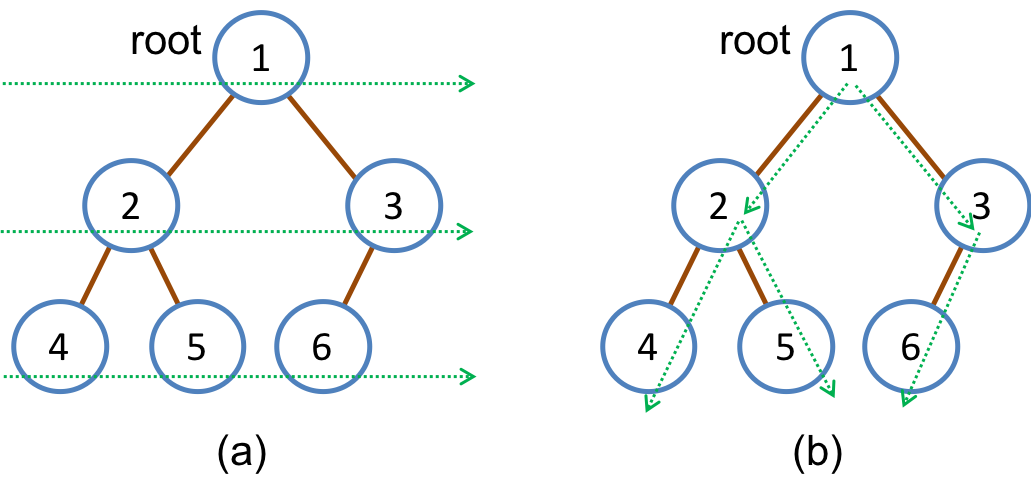
図10.2: (a)横型探索 と (b)縦型探索
ここでは,横型探索で木の節をたどることとし,heap-check.c に,以下に示す2つの関数を用意した.
(1) tree の節を横型探索でたどり,その順番で節を格納したキューを取得する.ただし,子が存在しない場合,その位置に ダミーの節(value の値が -1 の節)をキューの要素として格納している.
struct queue *traverse_bfs(struct tree *tree);
(2) tree の節を横型探索でたどり,節に格納された value の値を画面に表示する.
void print_bfs(struct tree *tree);
節を格納したキュー queue に対して,以下に示す2つの関数を利用すれば,木の節を取得することができる.
(3) queue の大きさを取得する.
int size_of_queue(struct queue *queue);
(4) queue の index 番目の要素を取得する.
struct node *get_in_queue(struct queue *queue, int index);
これらの関数を利用するためには,heaptree-common.h をインクルードし,heap-check.o と queue.o をリンクすること.
いま,以下の条件を満たす完全2分木をヒープ(heap)と呼ぶ.
- 木の節(のキーの値)に全順序関係があり,すべての節の間の順序が決定できる.
- 親の順序は子の順序より必ず前側にある.つまり,親のキーの値は子のキーの値よりも必ず小さいか等しい.
そこで,以下に示す関数を持つソースコード prog10-2.c を作成する.
(1) tree がヒープ条件を満たすかどうかを検査する.条件を満たす場合は 1,満たさない場合は 0 を返す.
int is_heaptree(struct tree *tree);
上記の関数とテストコードを含むprog10-2.cを作成せよ.
prog10-2.cには,完全2分木であるかどうかを検査する関数is_complete_binary_tree(struct tree *tree)を用意したので,参考にするとよい.
課題3: 配列による完全2分木の実現
完全2分木において節の数の上限があらかじめわかっている場合には,木構造を配列で表現することができる.
ここでは,heap-common.h で定義されている以下に示す構造体の配列を考える.
struct data {
int key;
char value;
};
完全2分木の節の数が num 個のとき,配列 data[] の大きさは num となる.ヒープの実装では,慣例的に,配列の添字を 1 から始めることになっている.よって,完全2分木の節は data[1]〜data[num] に格納される.
このような配列 data[] において,節 data[i] の左側の子は data[2*i],右側の子は data[2*i+1] となる.完全2分木と配列の対応関係を図10.3に示す.
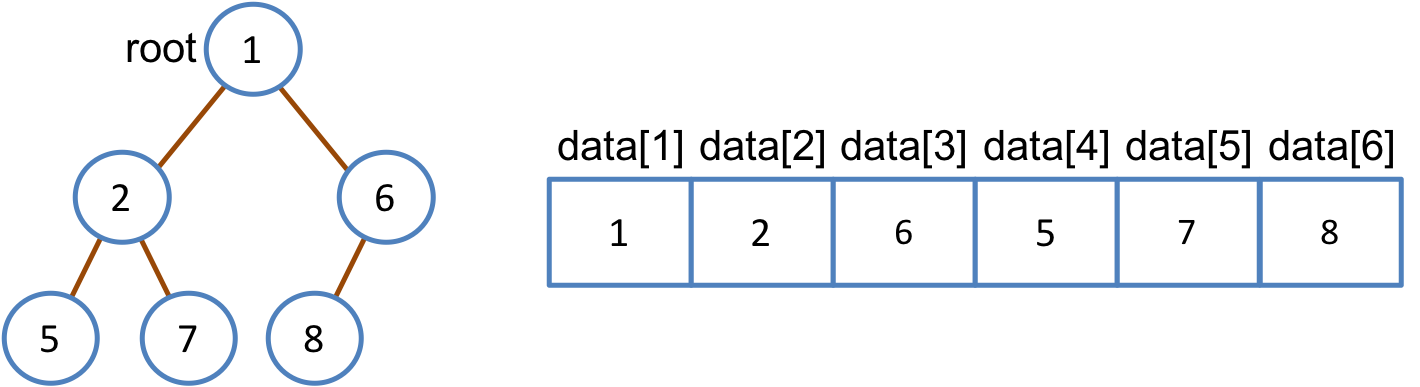
図10.3: 完全2分木と配列の対応
配列で表現した完全2分木に対して,以下に示す関数を持つソースコード prog10-3.c を作成する.
(1) data[] で表現された完全2分木がヒープ条件を満たすかどうかを検査する.条件を満たす場合は 1,満たさない場合は 0 を返す.num は完全2分木の節の数を指す.
int is_heap(struct data data[], int num);
上記の関数とテストコードを含むprog10-3.cを作成せよ.
data[0]は利用しないので,適当な値を格納しておくのでよい.また,data[]で表現された完全2分木の節を画面に表示するためには,ソースコードheap-check.cの関数print(int data[], int num)を利用するとよい.
課題4: ヒープソート
ヒープ条件を満たす配列 data[] において,先頭の要素 data[1] のキーの値は常に最小である.よって,この要素を順番に取り出していくことで,並び替えを実現することができる.このような方法をヒープソート(heap sort)と呼ぶ.
最小の要素を取り出した後でも,data[] が常にヒープ条件を満たすためには,要素の再構成が必要である.そこで,課題3で作成したソースコード prog10-3.c に対して,以下に示す2つの関数をソースコード prog10-4.c に用意した.
(1) data[] で表現された完全2分木に対して,data[index]の要素を根に向かって上方に移動させる.num は完全2分木の節の数を指す.
void shift_up(struct data data[], int num, int index);
(2) heap に格納されている data[] で表現された完全2分木に対して,data[index]の要素を葉に向かって下方に移動させる.num は完全2分木の節の数を指す.
void shift_down(struct data data[], int num, int index);
ここでは,struct data 型の配列 data[] に格納された整数の値 key をキーとして,ヒープソートにより配列の要素を降順に並び替える関数
void heap_sort(struct data data[], int num);を持つソースコード
prog10-4.c を作成する.a[1]〜a[num] の要素が並び替えの対象となる.
上記の関数とテストコードを含むprog10-4.cを作成せよ.
本課題では,テスト関数test1()がすでに用意されている.ソートの動作を検査するテストコードをprog10-4.cに追加せよ.
昇順でなく降順であること,さらに並び替え対象の範囲がいままでのソートの方法と異なることに注意せよ.
