第13回 - 探索(2)
第13回では,以下の項目に関して学ぶ.
- リストを用いた線形探索
- 2分探索木
課題1: リストを用いた線形探索
list-common.h で定義されている構造体の要素がランダムに並んでいる線形リストに対して.それぞれの要素に対して検索条件の成立を順番に調べる線形探索を考える.
struct data {
int key;
char value;
};
key は検索キー,value は格納されているデータを指す.
リストの要素は,list-common.h で定義されている以下の構造体で管理されている.
struct element {
struct data *data;
struct element *next;
};
この構造体は,後続する要素を指すポインタ next を持つ.要素が末尾の場合,next は NULL とする.
通常,リストは先頭から要素をたどるため,リストの先頭を指すポインタを用意する.ここでは,リストを list-common.h で定義されている構造体で表現する.
struct list {
struct element *top;
};
top はリストの先頭を指すポインタである.リストが空の場合,top は NULL とする.
いま,リストを用いた線形探索を実現するために,以下に示す2つの関数を用意する.
(1) 要素を格納する空の線形リストを生成する.
struct list *create_list();
(2) list に格納されている要素に画面に表示する.
void print(struct list *list);
これらの関数を利用するためには,list-common.h をインクルードし,list-check.o をリンクすればよい.
リストに格納された要素に対する線形探索を実現するために,以下に示す3つの関数を持つソースコード prog13-1.c を作成する.
(1) list に格納されているデータから,検索キー key を持つ要素を見つける.データが見つからなかった場合は NULL を返す.
struct data *search(struct list *list, int key);
(3) list に要素 data を追加する.すでに格納されている要素と同一の検索キーを持つ要素は追加できない.追加に成功した場合は 1,失敗した場合は 0 を返す.
int insert(struct list *list, struct data data);
(3) list から検索キー key に一致する要素を削除する.削除に成功した場合は 1,失敗した場合は 0 を返す.
int delete(struct list *list, int key);
上記の3つの関数とテストコードを含むprog13-1.cを作成せよ.
本課題では,テスト関数test1()がすでに用意されている.さまざまなリストに対して,探索を行うテストコードをprog13-1.cに追加せよ.
課題2: 2分木の探索
tree-common.h で定義されている以下の構造体で2分木を表現する.
struct node {
struct data *data;
struct node *left;
struct node *right;
int height;
};
left は左側の子へのポインタ,right は右側の子へのポインタ,data は格納するデータへのポインタを指す.子が存在しない場合は,left や right を NULL とする.height は,その節を頂点とする木の高さを指す.
struct data は,tree-common.h において,以下のように定義されている.
struct data {
int key;
char value;
};
key は検索キー,value は格納されているデータを指す.
いま,2分木を実現するために,tree-check.c に,以下に示す3つの関数を用意した.
(1) 空の2分木(根を持たない)を生成する.
struct tree *create_tree();
(2) キーの値 key とデータ value を格納した節を生成する.
struct node *create_node(int key, char value);
(3) tree の節に格納されているキーの値とデータを画面に表示する.
void print(struct tree *tree);
ここでは,2分木の縦型探索(深さ優先)を取り上げ,以下に示す3つの関数を持つ prog13-2.c を作成する.
(1) tree を縦型に探索し,行きがけ順(先行順)に節を集める.集めた節はキュー queue に格納する.
void traverse_dfs_preorder(struct node *node, struct queue *queue);
(2) tree を縦型に探索し,通りがけ(中間順)に節を集める.集めた節はキュー queue に格納する.
void traverse_dfs_inorder(struct node *node, struct queue *queue);
(3) tree を縦型に探索し,帰りがけ順(先行順)に節を集める.集めた節はキュー queue に格納する.
void traverse_dfs_postorder(struct node *node, struct queue *queue);
これらの関数を作成する際には,tree-common.h をインクルードし,heap-check.o と queue.o をリンクすること.
上記の3つの関数とテストコードを含むprog13-2.cを作成せよ.
本課題では,テスト関数test1(),test2(),test3()がすでに用意されている.探索の動作を検査するテストコードをprog13-2.cに追加せよ.
課題3: 2分探索木
2分木の節(のキーの値)に全順序関係があり,以下の条件を満たす場合に,この木を2分探索木(binary search tree)呼ぶ.
- ある節 v の順序は左側の子の子孫の順序より必ず後ろ側である.つまり,親のキーの値は左側の子の子孫のキーの値よりも必ず大きい.
- v の順序は右側の子の子孫の順序より必ず前側である.つまり,親のキーの値は右側の子の子孫のキーの値よりも必ず小さい.
2分探索木の例を図13.1に示す.
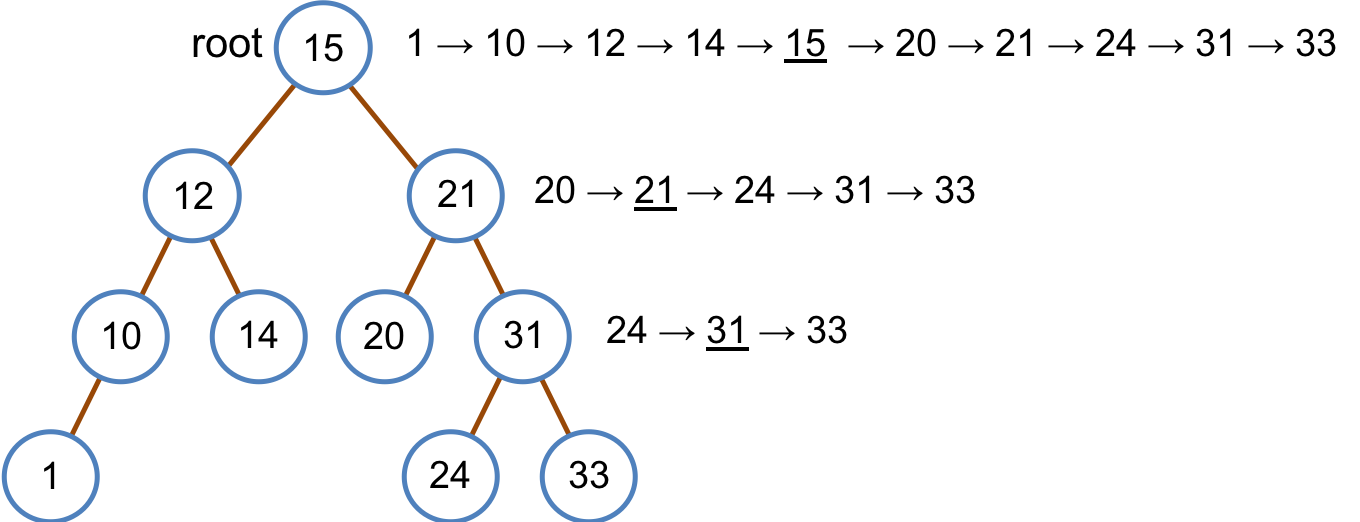
図13.1: 2分探索木の例
図13.1において,キーの値が15である節を頂点とする木を見ると,その節の右側の節のキーの値は必ず15より小さく,右側の節のキーの値は必ず15より大きくなっていることがわかる.また,キーの値が21の部分木を見ると,その節の右側の節のキーの値は必ず21より小さく,右側の節のキーの値は必ず21より大きくなっていることがわかる.
2分探索木の条件より,縦型探索の節を通りがけ順にたどると,必ず昇順の列が取得できる.このことを利用して,以下に示す関数を持つソースコード prog13-3.c を作成する.
(1) tree が2分探索木であるかどうかを検査する.2分探索木の場合は 1,2分探索木でない場合は 0 を返す.
int is_binary_search_tree(struct tree *tree);
上記の関数とテストコードを含むprog13-3.cを作成せよ.
課題4: 2分探索木の操作
prog13-3.c に対して,以下に示す3つの関数を追加した prog13-4.c を作成する.
(1) tree において,検索キー key を持つ節を見つける.節が見つからなかった場合は NULL を返す.
struct data *search(struct tree *tree, int key);
(2) tree にデータ data を格納した節を追加する.すでに格納されている節と同一の検索キーを持つ節は追加できない.追加に成功した場合は 1,失敗した場合は 0 を返す.
int insert(struct tree *tree, struct data data);
(3) tree から検索キー key に一致する節を削除する.削除に成功した場合は 1,失敗した場合は 0 を返す.
int delete(struct tree *tree, int key);
上記の3つの関数とテストコードを含むprog13-4.cを作成せよ.
本課題では,テスト関数test1()がすでに用意されている.さらに,テストコードをprog13-4.cに追加せよ.
課題5: 平衡木
木において,節から任意の葉に到達する際に通る枝の数の最大値を,その節の高さという.2分探索木による探索では,各節を頂点とする左右の部分木のバランスが取れている場合にもっとも効率的に検索が実行できる.しかしながら,節の挿入の順序によっては,必ずしもバランスのよい木が構築できるとは限らない.
2分探索木のすべての節において,左側の子を頂点とする部分木と右側の子を頂点とする部分木の高さの差がなるべく等しくなるように構築された木を平衡木(balanced tree)という.
ここでは,高さの差が1以内に収まるAVL木(Adelson-Velskii and Landis' tree)を取り上げ,以下に示す3つの関数を含む prog13-5.c を作成する.
(1) tree において,検索キー key を持つ節を見つける.節が見つからなかった場合は NULL を返す.
struct data *search(struct tree *tree, int key);
(2) tree にデータ data を格納した節を追加する.すでに格納されている節と同一の検索キーを持つ節は追加できない.追加に成功した場合は 1,失敗した場合は 0 を返す.
int insert(struct tree *tree, struct data data);
(3) tree から検索キー key に一致する節を削除する.削除に成功した場合は 1,失敗した場合は 0 を返す.
int delete(struct tree *tree, int key);
(3) tree がAVL木であるかどうかを検査する.AVL木の場合は 1,AVL木でない場合は 0 を返す.
int is_AVL_tree(struct tree *tree);
上記の4つの関数とテストコードを含むprog13-5.cを作成せよ.
