第15回 - グラフ
第15回では,以下の項目に関して学ぶ.
- グラフとその表現
- グラフに対する深さ優先探索と幅優先探索
課題1: グラフの表現
対象とそれらの関係を抽象的に表現するのに適したデータ構造にグラフ(graph)がある.グラフは,頂点(vertex)の集合と頂点を結ぶ辺(edge)の集合で構成される.辺に方向がない場合を無向グラフ(undirected graph),辺に方向がある場合を有向グラフ(directed graph)と呼ぶ.それぞれのグラフを図15.1に示す.
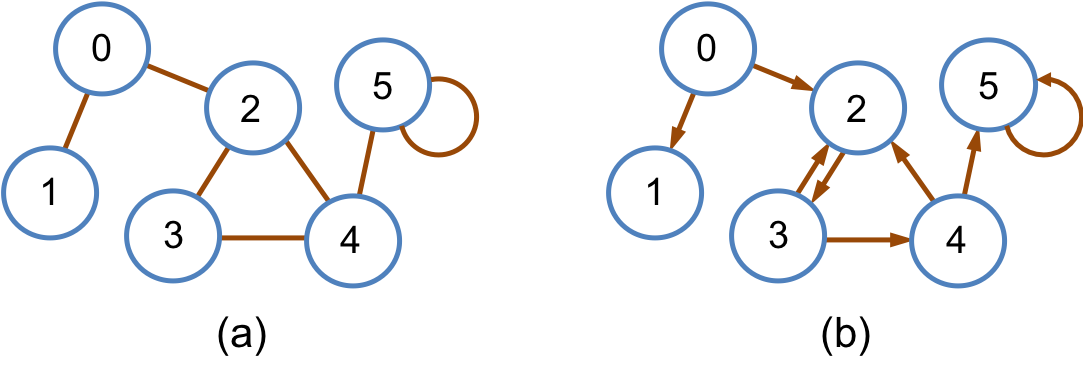
図15.1: (a) 無向グラフ と (b) 有向グラフ の例
ここでは,頂点の集合 V と辺の集合 E で構成される有向グラフ G = (V, E) を考える.2つの頂点 v ∈ V と u ∈ V に対して,それらを結ぶ辺を e = (v, u) ∈ E とおく.このとき,v と u は隣接する(adjacent)という.特に,有向グラフのとき,v を始点(source),u を終点 (destination) と呼ぶ.
グラフの実現方法には,隣接行列(adjacenct matrix)と隣接リスト(adjacency list)がある.
隣接行列では,頂点 v と 頂点 u に(有向)辺がある場合に,行例の(v, u) 要素の値を 1,(有向)辺がない場合に 0 とする.図15.1(b)の有向グラフの隣接行列による表現を図15.2(a)に示す.行列を2次元配列 matrix[][] で実現した場合,matrix[v][u] の値が 1 か 0 となる.
一方,隣接リストでは,頂点 v に対して,最大|V|個の隣接頂点 u をリストで実現する.図15.1(b)の有向グラフの隣接リストによる表現を図15.2(b)に示す.
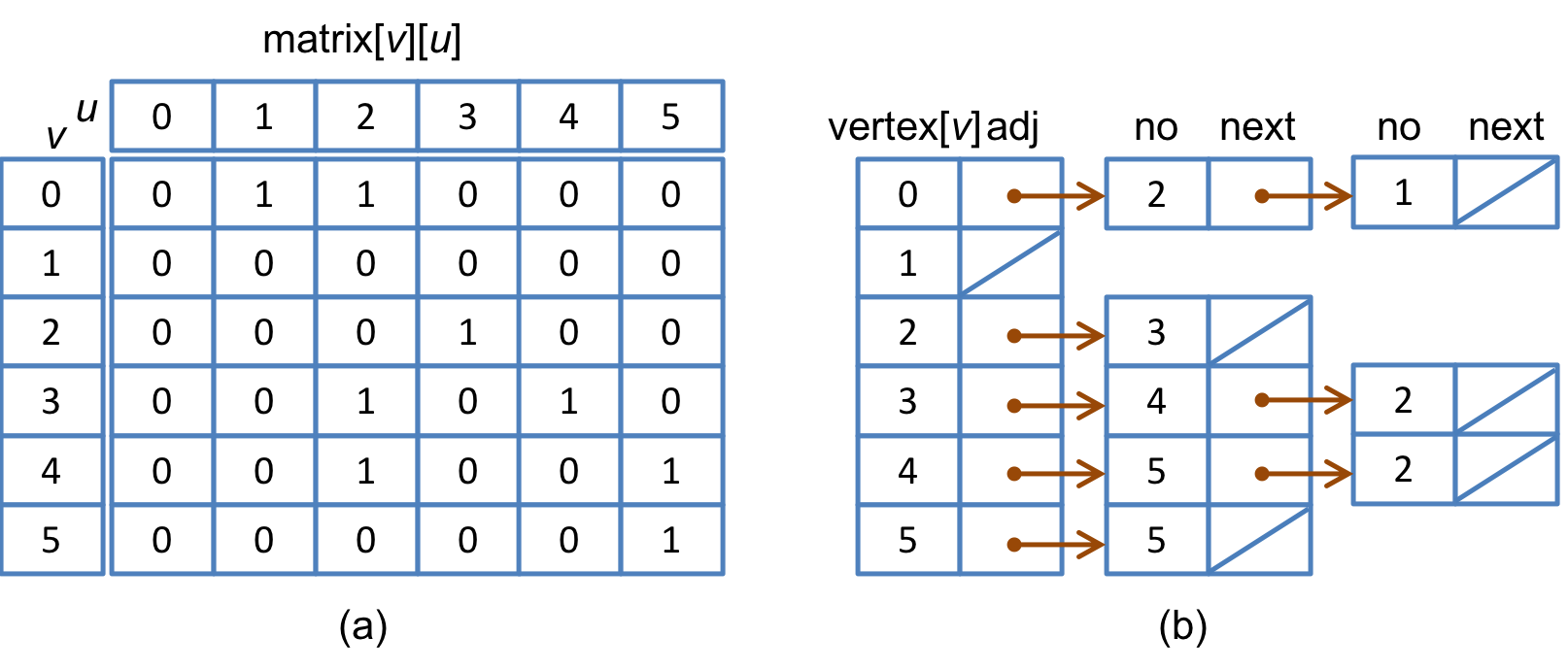
図15.2: (a) 隣接行列による表現と (b) 隣接リストによる表現 の例
グラフの頂点を graph-common.h で定義されている以下の構造体で実現する.
struct vertex {
int no;
char label;
struct adjacence *adj;
};
no は頂点の識別番号,label は頂点のラベル(頂点に格納するデータ),adj は隣接リストの先頭のポインタを指す.隣接頂点が存在しない場合は,adj を NULL とする.
struct adjacence は,以下のように定義されている.
struct adjacence {
int no;
struct adjacence *next;
};
no は頂点の識別番号,next は隣接頂点の識別番号を格納する構造体オブジェクトへのポインタを指す.
いま,グラフを実現するために,graph-check.c に,以下に示す3つの関数を用意した.
(1) 空のグラフ(頂点と辺を持たない)を生成する.
struct graph *create_graph();
(2) graph の隣接行列を画面に表示する.
void print_matrix(struct graph *graph);
(3) graph の隣接リストを画面に表示する.
void print_list(struct graph *graph);
ここでは,有向グラフに対して,以下に示す4つの関数を持つ prog15-1.c を作成する.
(1) ラベルの値 label を格納した頂点を生成し,graph に追加する.生成した頂点へのポインタを返す.
struct vertex *add_vertex(struct graph *graph, char label);
(2) 頂点 src と を結ぶ辺を生成し,graph に追加する.
graph に追加する.void add_edge(struct graph *graph, struct vertex *src, struct vertex *dst);
(3) graph に含まれる頂点の総数を取得する.
int get_vertex_num(struct graph *graph);
(4) graph に含まれる辺の総数を取得する.
int get_edge_num(struct graph *graph);
これらの関数を作成する際には,graph-common.h をインクルードし,graph-check.o をリンクすること.
上記の4つの関数とテストコードを含むprog15-1.cを作成せよ.
本課題では,図15.1(b)の有向グラフを構築し,隣接行列と隣接リストの正しさを確認するテスト関数test1()を作成せよ.さらに,図15.1(b)以外の有向グラフを構築するテスト関数を追加せよ.
課題2: グラフに対する深さ優先探索
ある頂点(始点) v に対して未訪問の隣接頂点(終点) u が存在する場合,uを次の始点として探索をつづける戦略を深さ優先探索(DFS: depth-first search)という.u の隣接頂点がすべて訪問ずみとなった際.u を訪問する直前の頂点 v に戻り,再帰的に探索を続ける.
ここでは,prog15-1.c に対して,スタックを用いることで深さ優先探索を実現することとし,以下に示す関数を追加した prog15-2.c を作成する.
(1) graph の頂点を深さ優先探索で訪問し,訪問順に集めた頂点の列(配列へのポインタ)を取得する.start は探索を開始する頂点を指す.
struct vertex **visit_dfs(struct graph *graph, struct vertex *start);
ただし,ある頂点に対して複数の隣接頂点が存在する場合,頂点の識別番号が小さい順に訪問する.
上記の関数とテストコードを含むprog15-2.cを作成せよ.
スタックを利用するには,stack.hをインクルードし,stack.oをリンクすること.
また,訪問順に集めた頂点の列を確認するために,graph-check.c に,以下に示す関数を用意した.
(1) 頂点の列を画面に表示する.vertex は頂点の配列へのポインタを指す.
void print_trajectory(struct vertex **vertex);
この関数を作成する際には,graph-common.h をインクルードし,graph-check.o をリンクすること.
課題3: グラフに対する幅優先探索
ある頂点(始点) v に対して未訪問の隣接頂点(終点) u が存在する場合,u を優先的に探索する戦略を幅優先探索(BFS: breadth-first search)という.v の隣接頂点がすべて訪問ずみとなった際.v の隣接頂点の一つを次の始点として探索をつづける.
ここでは,prog15-1.c に対して,キューを用いることで幅優先探索を実現することとし,以下に示す関数を追加した prog15-3.c を作成する.
(1) graph の頂点を幅優先探索で訪問し,訪問順に集めた頂点の列(配列へのポインタ)を取得する.start は探索を開始する頂点を指す.
struct vertex **visit_bfs(struct graph *graph, struct vertex *start);
ただし,ある頂点に対して複数の隣接頂点が存在する場合,頂点の識別番号が小さい順に訪問する.
上記の関数とテストコードを含むprog15-3.cを作成せよ.
キューを利用するには,queue.hをインクルードし,queue.oをリンクすること.
また,訪問順に集めた頂点の列を確認するために,関数 print_trajectory(struct vertex **vertex) を利用するとよい.
課題4: 重み付きグラフと最短経路
グラフの辺に重み(コスト)を付けたものを重み付きグラフ(weighted graph)と呼ぶ.重み付きグラフを隣接行列 M により表現する場合,頂点 v と頂点 u を結ぶ辺を表す M[v][u] にその辺の重みを設定すればよい.辺が存在しない場合は,M[v][u] の値を無限大とする.図15.3に,
重み付きグラフとその隣接行列を示す(*は無限大を指す).
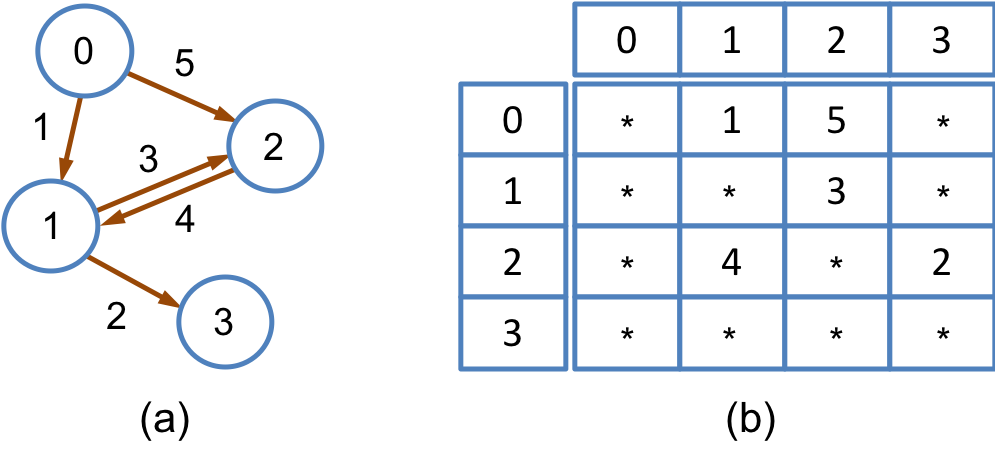
図15.3: (a) 重み付きグラフと (b) 隣接行列による表現 の例
最短経路(shortest path)とは,重み付きグラフにおいて,頂点 v から 頂点u に到達する経路の中で,辺の重さの総和が最小の経路を指す.
ここでは,与えられた1つの頂点から他の頂点への最短経路を求めるために,以下の関数を持つソースコード prog15-4.c を作成する.
いま,グラフを実現するために,graph-check.c に,以下に示す3つの関数を用意した.
(1) 空の重み付きグラフ(頂点と辺を持たない)を生成する.辺が存在しない場合,隣接行列の各要素の重みは,limits.h で定義されている INT_MAX とする.
struct graph *create_weighted_graph()
(2) ラベルの値 label を格納した頂点を生成し,graph に追加する.生成した頂点へのポインタを返す.
struct vertex *add_vertex(struct graph *graph, char label);
(3) 頂点 src と を結ぶ辺を生成し,graph に追加する.weight は辺の重みを指す.
graph に追加する.weight は辺の重みを指す.void add_edge(struct graph *graph, struct vertex *src, struct vertex *dst, int weight);
(4) graph における頂点 start から,graph上のそれぞれの頂点に到達する経路の重みの総和を格納した配列を取得する.
int *shortest_path(struct graph *graph, struct vertex *start);
ただし,始点と終点が同じ場合の重みの総和は 0 とする.
上記の関数とテストコードを含むprog15-4.cを作成せよ.
本課題では,3つのテスト関数test1(),test1(),test3()がすでに用意されている.他のテスト関数を追加せよ.
ダイクストラ(E. W. Dijkstra)のアルゴリズムを用いることができる.
